好久以前不记得在那本初赛资料上看到第一章就是博弈论,看了一页纸,~~(那时候还不知道有多难,就只是感性地用数学去理解)~~,感觉不难,就没搞了。
考了好几次博弈论的题,发现毛都不会,又老听旁边 $Mital$ 和 $Skounputer$ 讲什么 $SG$ 函数,心态爆炸,于是还是决定自己学一下。
蒟蒻决定先把几个经典的例子学会了,再去考虑有没有什么可以合并总结的吧。 **** **** **参考:**
**https://www.cnblogs.com/zwfymqz/p/8460196.html**
**https://www.cnblogs.com/Mathics/p/3948482.html**
**https://www.luogu.org/blog/skounputer/bo-yi-lun-xiao-jie**
**https://www.luogu.org/blog/155767/shuo-lun-xiao-jie**
**** **** ## 一、巴什博弈 ~~(当年我看的就是这个,贼简单,所以就没往后学了QAQ)~~
> 模型:给定一堆 $n$ 个石头,两个人博弈,依次取 $[~1,m~]$ 个石头,若不能取了,则当前操作者输。问是否必胜?
### 模拟讨论: $\quad(1)$如果当前有 $1$ ~ $m$ 个石子,那么显然先手一定能一次性全部取完,先手必胜。
$\quad$于是我们考虑什么时候起先手不一定必赢呢?
$\quad(2)$如果当前正好有 $m+1$ 个石子,因为先手至少取一个但又不能完全取完,所以会留下 $1$ ~ $m$ 个石子给后手处理,后手显然是可以一次性取完的,所以先手必败。
$\quad(3)$如果我们再多几个石子 $(~\le m~)$ ,那么显然先手可以把石子数取到 $m+1$ 的状态,即状态 $2$ ,由于此时的先手,即整场的后手在状态 $2$ 下必败,所以先手必胜。
### 结论: $\quad$发现了吗?只要 $n$ 不为 $m+1$ 的倍数,那么每次先手只要把石子数取到 $m+1$ 的倍数,就能使下一个操作者即后手必败,即自己必胜。
$\quad$这里,我们把 $m+1$ 称为必败态。那么我们可以发现,对于一个当前状态,如果他已经是必败态了,那么当前操作者必输;如果下一步可以使状态转移到必败态,那么下一个操作者必败,则当前操作者必胜。
$\quad$要注意的是,无论是必败态还是必胜态,他都仅仅是一个状态,表示当前操作者胜负的状态,而与操作者是谁无关。
$\quad$很显然我们又可以发现,对于每一个石子个数即每一个状态,我们可以唯一的知道他是必胜态还是必败态,即他要么是必败态要么是必胜态,不会有不一定这一种状态。那么我们应该怎么得到它是什么状态呢?
$\quad$这里我们可以使用一棵树来表示对于当前的 $n$ 的所有的操作。
$\quad$这是 $n=3,m=2$ 的情况下的操作树。
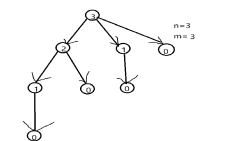
$\quad$显然,我们发现有许多的状态使重复的,于是我们可以把树精简为一张有向无环图。如下:
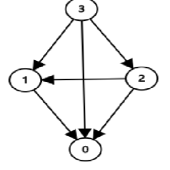
$\quad$我们从 $0$ 开始向上递归。
$\quad$因为 $0$ 是必败态(先手已经没有可取的了,直接输),所以能够转换到他的状态 $1,2$ 是必胜态(因为 $1,2$ 的下一步可以直接转到必败态 $0$ ,所以下一个操作者必败,即当前操作者必胜),而 $3$ 也是必胜态,(他能转换到必败态 $0$ ,因为所有操作者都非常聪明,所以先手一定会选择这一个方案,所以当前操作者必胜)。
$\quad$由上,我们又可以发现,如果一个状态可以转移到必败态,那么他一定是必胜态,无论他还可不可以转移到别的必胜态;如果一个状态所能转移到的状态全都是必胜态,即没有必败态,那么他一定是必败态。
*** *** *** 综上,我们得到了只有一个操作空间(即只有一堆石头)时的做法。但是有的时候我们有很多个操作空间(即有很多堆石子),届时我们该怎么办呢? *** *** *** ## 二、Nim游戏 >模型:有n堆石子,可以从任意一堆中拿若干个石子(不能不拿),没法拿的人失败。问谁会胜利?
### 模拟讨论
$\quad$我们按照套路,从简单的情况入手。
$\quad$当只有一堆石子的时候,先手可以全部拿走,先手必胜,为必胜态。。
$\quad$当有两堆石子且石子个数相同的时候,先手不论拿多少,后手都可以从另一堆中拿同样多的石子,那么无论如何第一堆的最后一个是先手拿的,则下一状态为后手操作下的必胜态,先手必败,为必败态;否则(两堆石子数不同),那么先手可以把石子数取到两堆相同,下一状态则为后手操作下的必败态(两堆石子数相同),先手必胜。
$\quad$当有三堆的时候呢?
$\quad$当有n堆的时候呢?
$\quad$这样玩下去确实是很繁琐,不过前辈们总结出了一条非常厉害的规律!
### 定理: >当 $n$ 堆石子的个数的异或和等于 $0$ 的时候,先手必败,否则先手必胜。
为什么呢?
证明如下:
> 设每堆石头个数分别为 $a_1,a_2...a_n$ ,异或符号为 $\oplus$ 。 > > 如果 $a_1 \oplus a_2 \oplus ... \oplus a_n=0$ ,那么无论先手怎么取,后手只要取掉一部分石头来维持异或和为 $0$ 。最后只剩一个堆有石头的时候,异或和不为零为这一堆的石子个数,那么此时就是后手的回合,他可以一波取完,所以异或和为 $0$ 的状态为当前操作者的必败态。 > > 我们设石头堆数量异或和为 $S(~S!=0~)$ ,那么 $a_1 \oplus a_2 \oplus ... \oplus a_n=S$ 。 > > 设 $S$ 的二进制最高位为第 $k$ 位,那么一定存在至少一个 $a_i$ 的第 $k$ 位为 $1$ ,否则异或和的最高为不可能为 $1$ 。 > > 所以我们把等式左右同时异或上 $S$ ,则等式左边为 $0$ ,所以当前状态为当前操作者即后手的必败态; > > 而这个异或的操作,由于 $a_i$ 和 $S$ 的最高位都是 $1$ ,那么异或后最高位结果就是 $0$ ,显然是比原数要小,所以我们可以视为第 $i$ 个石头堆被取走了一些石头使他变成了 $a_i \oplus S$ 个石头。 > > 综上,如果所有石头堆的异或和为 $0$ ,那么为先手的必败态;否则为先手的必胜态。
### 引申:nimk游戏 >模型:n堆石子,每次从不超过k堆中取任意多个石子,最后不能取的人失败。
**** **** **** ## 三、SG函数与SG定理 $这个很重要!!!$
### SG函数 > 定义: $SG(~x~)=mex(~v1,v2,...vm~)$ > > 其中 $v$ 表示当前 $x$ 可以转移到的状态的 $SG$ 值, $mex$ 表示在这个集合中没出现的最小自然数。 > > 其中,如果 $SG(~x~)==0$ ,表示他可以转移到必败态,即他的下一个状态可以是必败态,则状态 $x$ 为必胜态。否则反之。
### SG定理 > 内容:对于一个问题,如果存在很多个操作空间,其 $SG$ 值分别为 $SG_1,SG_2...SG_n$ 。 > 如果 $SG_1 \oplus SG_2 \oplus ... \oplus SG_n==0$ ,则先手必输。
你一定会惊呼:这不就是 $nim$ 游戏吗?
重看 $num$ 游戏,你会发现其中每堆石子的 $SG$ 值都恰好为这堆石子的数量,且每堆石子之间都是相互独立的。
所以$nim$游戏可以当作对 $SG$ 定理的一个很好的证明。
### SG的本质
看到这里,有些读者可能要问了:我们为什么要用 $mex$ 来定义 $SG$ 函数呢?对于 $nim$ 游戏来说 $SG$ 的值就是石子个数,那么其他的博弈问题呢? $SG$ 函数还有用吗?为什么呢?
我们回到一开始的巴什博弈——如果把他拓展到多个操作空间要怎么解决呢?
首先把巴什博弈看作一张有向无环图
这里给出的本质是 **SG的本质应该是将n维Nim游戏映射到1维Nim游戏**
虽然还不是太懂,但还是先放在这里吧。$QAQ$
综上,**SG函数的真正目的是将复杂的博弈问题分解成一个个独立的博弈问题之后,通过SG函数将其转化为一个个Nim游戏,然后利用Bouton's Theorem (即将 SG 值异或和)求出整个博弈问题的解。这也就是Sprague-Grundy定理。SG函数的定义就是根据Nim游戏的性质构造出来的一个函数,可以将普通的博弈问题转化为Nim问题,而Nim问题一定有解,故相应博弈问题也一定有解。**