原文链接:这里
0.前言
I—MR图(单值—移动极差)控制图。
使用 I-MR 控制图 可以在拥有连续数据且这些数据是不属于子组的单个观测值的情况下监视过程的均值和变异。使用此控制图可以监视过程在一段时间内的稳定性,以便可以标识和更正过程中的不稳定性。
注意:数据必须呈现合理的正态分布。
mintab中文支持网站:https://support.minitab.com/zh-cn/minitab
mintab破解版下载地址:
首先一些名词解释:
- 标准差:是方差的算术平方根。
- 方差:每个样本值与全体样本值的平均数之差的平方的平均数。
- UCL:控制上限
- LCL:控制下限
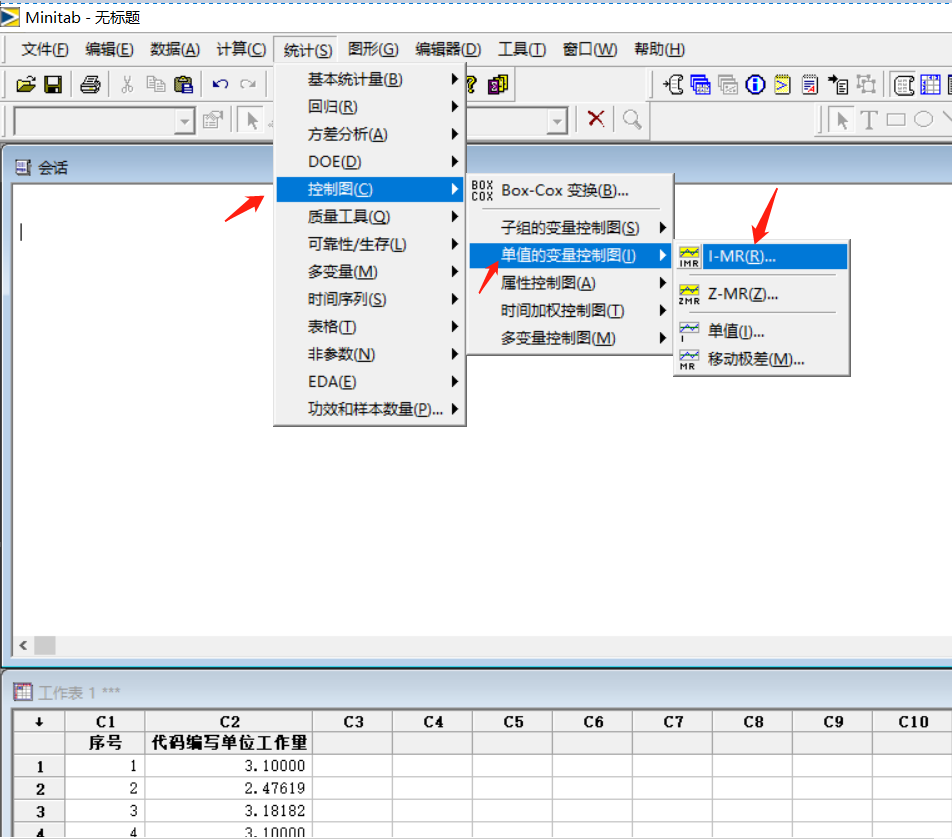
1.如何使用mintab创建I—MR控制图
本文使用的mintab17版本
(1)参考数据(收集的数据最好>=25,数据太少没有参考意义)
| 编号 | 数值 | |
| 1 | 3.10 | |
| 2 | 2.47 | |
| 3 | 3.18 | |
| 4 | 3.10 | |
| 5 | 2.48 | |
| 6 | 3.07 | |
| 7 | 2.46 | |
| 8 | 3.11 | |
| 9 | 2.68 | |
| 10 | 3.30 |
(2)生成图形
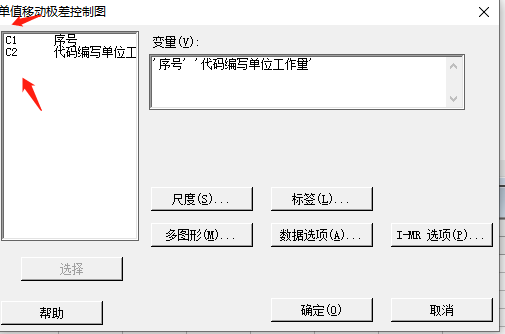
双击左侧的C1和C2,值就会去右侧
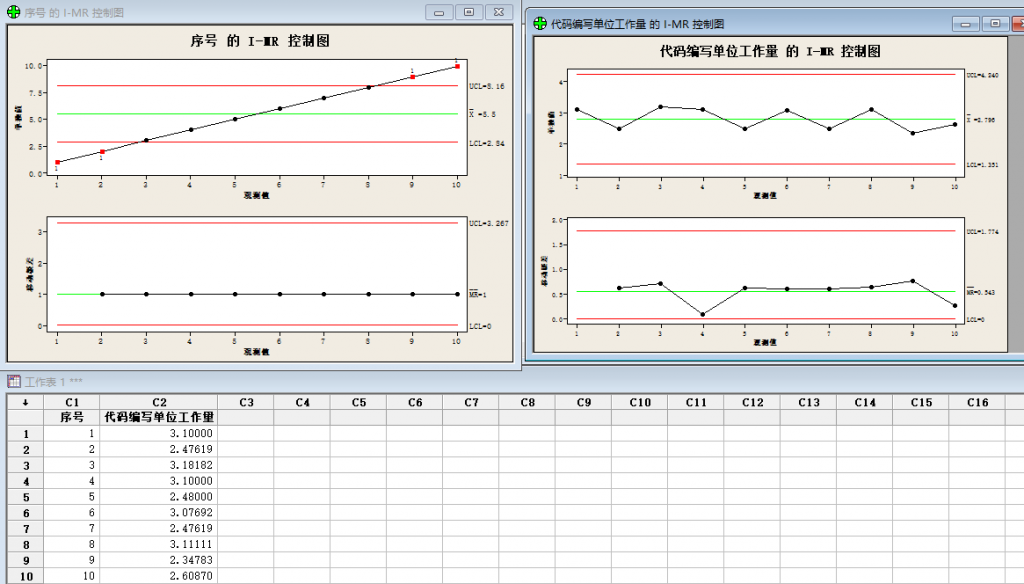
这个时候点击”确定“就会生成我们选中的两个I—MR图,
但是这个图并不是我最终想要的,因为做这个控制图是想找到数据异常点,想单位代码编写工作量没有异常点。所以我们还需要继续改参数。
2.修改参数
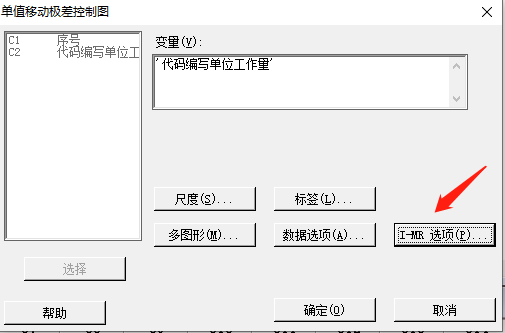
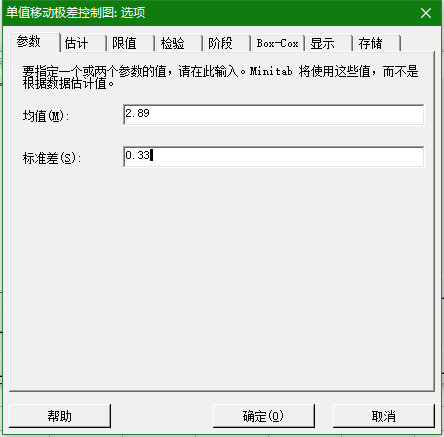
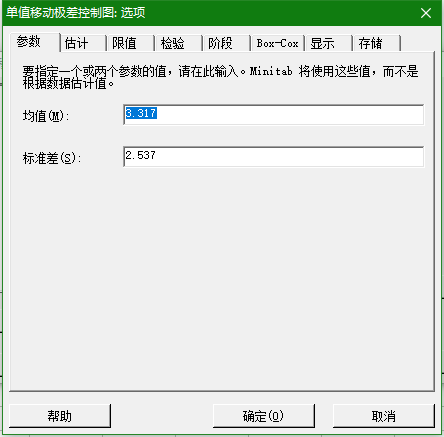
(1)我们主要修改I—MR选项
我们需要修改一些参数 ,在这个地方填入均值和标准差。
注:均值和标准差的计算过程可以参考下面:
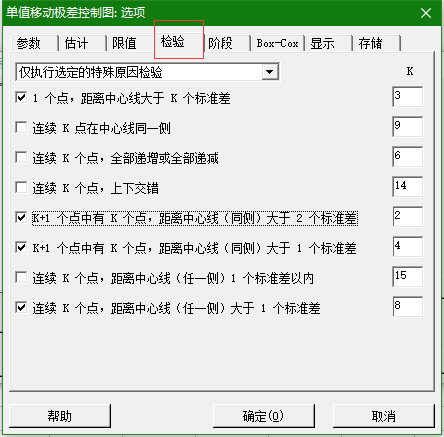
(2)设置判断异常点的规则:
设置判断异常点的规则也就是怎样去识别数据中不稳定的过程。我们一般遵循8—4—2—1法则。(也就是上图我选中的部分)
- 单独一个点掉出3 σ范围之外
- 3个连续的点里有至少2个点在中值的同一侧并且掉在2σ之外
- 5个连续点至少有4个点在中值的同一侧并且掉在1σ之外
- 至少8个连续的点掉在中值同一侧
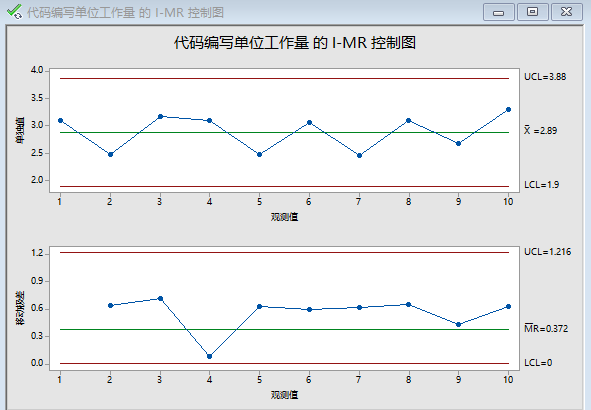
注意,判异规则是自己组织定义的,可以改动,规则并不唯一。然后点击确定可以生成下面的图图像,可以看出图像没有任何异常点,下面我们故意加入异常点,看能否识别出来。
3.增加异常点分析数据
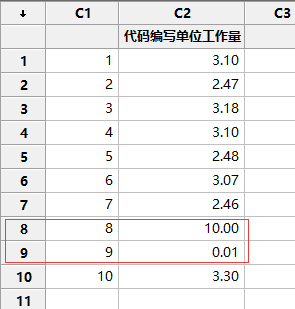
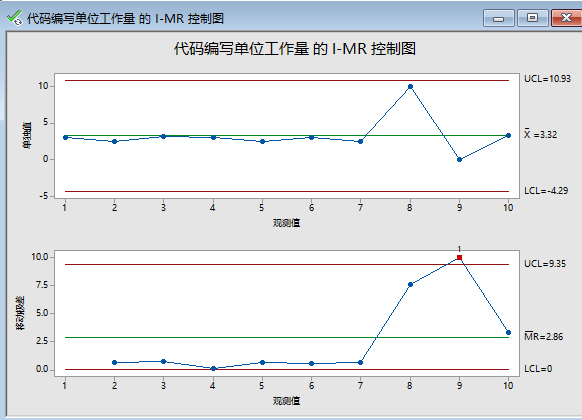
上面的数据没有异常点,我们在这里故意设置一个异常点, 看其是否能够筛选出。我们修改两个点,如下图:
重新计算均值和标准差得
然后,点击确定,出现控制图,这个时候有个红点出现了,表示根据我们的规则,出现了异常数据。