?
2021 年高教社杯全国大学生数学建模竞赛题目
（请先阅读“全国大学生数学建模竞赛论文格式规范”）
D 题 连铸切割的在线优化
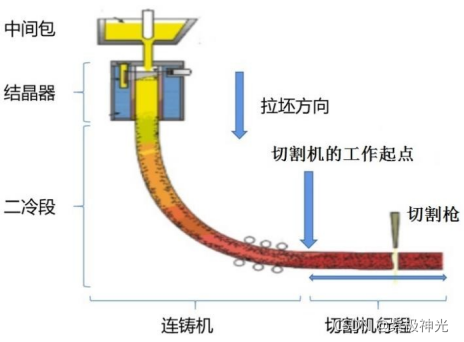
连铸是将钢水变成钢坯的生产过程，具体流程如下（图 1）：钢水连续地从中间包浇入结晶器， 并按一定的速度从结晶器向下拉 出，进入二冷段。钢水经过结晶 器时，与结晶器表面接触的地方 形成固态的坯壳。在二冷段，坯 壳逐渐增厚并最终凝固形成钢坯。然后，按照一定的尺寸要求对钢坯 进 行 切 割 。?
图 1 连 铸 工 艺 的 示 意 图
在连铸停浇时，会产生尾坯，尾坯的长度与中间包中剩余的钢水量及其他因素有关。因此，尾坯的切割也是连铸切割的组成部分。
切割机在切割钢坯时，有一个固定的工作起点，钢坯的切割必须从工作起点开始。在切割过程中，切割机骑在钢坯上与钢坯同步移动，保证切割线与拉坯的方向垂直。在切割结束后，再返回到工作起点，等待下一次切割。
在切割方案中，优先考虑切割损失，要求切割损失尽量小，这里将切割损失定义为报废钢坯的长度；其次考虑用户要求，在相同的切割损失下，切割出的钢坯尽量满足用户的目标值。
在浇钢过程中，结晶器会出现异常。这时，位于结晶器内部的一段钢坯需要报废，称此段钢坯为报废段（图 2）。当结晶器出现异常时，切割工序会马上知道，以便立即调整切割方案。?
图 2 钢坯出现报废段的示意图
切割后的钢坯在进入下道工序时不能含有报废段。当钢坯出现报废段时，先通过切割机切断附着有报废段的钢坯，然后通过离线的二次切割，使余下的钢坯
符合下道工序要求的长度；其他进入下道工序的钢坯也必须满足下道工序的长度要求。
现请你们团队建立数学模型或设计算法，解决以下问题：
问题 1 在满足基本要求和正常要求的条件下，依据尾坯长度制定出最优的切割方案。假定用户目标值为 9.5 米，目标范围为 9.0~10.0 米，对以下尾坯长度：109.0、93.4、80.9、72.0、62.7、52.5、44.9、42.7、31.6、22.7、14.5
和 13.7（单位：米），按“尾坯长度、切割方案、切割损失”等内容列表给出具体的最优切割方案。
问题 2 在结晶器出现异常时，给出实时的最优切割方案：(1)在钢坯第 1次出现报废段时，给出此段钢坯的切割方案；(2)在出现新的报废段后（如图 2），给出新一段钢坯的切割方案和当前段钢坯切割的调整方案，或声明不作调整。 假设结晶器出现异常的时刻在 0.0、45.6、98.6、131.5、190.8、233.3、 266.0、270.7 和 327.9（单位：分钟），用户目标值是 9.5 米，目标范围是 9.0~10.0米。在满足基本要求和正常要求的条件下，按“初始切割方案、调整后的切割方案、切割损失”等内容列表给出这些时刻具体的最优切割方案。
问题 3 假设实时最优切割方案和结晶器出现异常的时刻均与问题 2 相同， 在满足基本要求和正常要求的条件下，对（1）用户目标值是 8.5 米，目标范围是 8.0~9.0 米,（2）用户目标值是 11.1 米，目标范围是 10.6~11.6 米两种情况分别按“初始切割方案、调整后的切割方案、切割损失”等内容给出具体的最优切割方案。
附录：参数与要求
工艺参数：切割机切断一块钢坯的时间为 3 分钟，切割后，返回到工作起点的时间为 1 分钟。从结晶器中心到切割机工作起点处钢坯的长度是 60.0 米，连铸拉坯的速度为 1.0 米/分钟。当结晶器出现异常时，报废段的长度是 0.8 米。基本要求：切割后的钢坯长度必须在 4.8~12.6 米之间，否则无法运走，阻碍生产。下道工序能够接受的钢坯长度是 8.0~11.6 米，如果不在此范围内，可以将钢坯运走进行二次离线切割，但切割下的部分报废，从而产生损失。例如，12.6 米的钢坯切掉 1.0 米变成 11.6 米，切下来的 1.0 米报废；而小于 8.0 米的钢坯只能全部报废。
正常要求：正常切割是按照用户要求的长度进行切割。用户要求包含目标值和目标范围，钢坯的切割长度应尽量满足目标值，而在目标范围内的长度也是可以接受的。例如，目标值是 9.5 米，目标范围是 9.0~10.0 米，则切割长度尽量是 9.5 米，而在 9.0~10.0 米之间的长度是允许的。当钢坯长度不在目标范围内时，会产生损失。例如，钢坯长度是 11.6 米，多出来的 1.6 米报废。
备注：
?
?