python信用评分卡(附代码,博主录制)
Before we tackle how to handle them, let’s quickly define what an outlier is. An outlier is any data point that is distinctly different from the rest of your data points. When you’re looking at a variable that is relatively normally distributed, you can think of outliers as anything that falls 3 or more standard deviations from its mean. While this will suffice as a working definition, keep in mind that there’s no golden rule for defining what an outlier is.
In general, outliers belong to one of two categories: a mistake in the data or a true outlier. The first type, a mistake in the data, could be as simple as typing 10000 rather than 100.00 – resulting in a big shift as we’re analyzing the data later on. The second type, a true outlier, would be something like finding Bill Gates in your dataset. His profile probably looks so different from the other people in your list that including him might skew your results. It’s important to distinguish these types because we’ll handle them differently in an analysis. It’s subjective. It’s up to you as the analyst to determine which data points are outliers in any given dataset.
Now, how do we deal with outliers? Here are four approaches:
1. Drop the outlier records.
In the case of Bill Gates, or another true outlier, sometimes it’s best to completely remove that record from your dataset to keep that person or event from skewing your analysis.
2. Cap your outliers data.
Another way to handle true outliers is to cap them. For example, if you’re using income, you might find that people above a certain income level behave in the same way as those with a lower income. In this case, you can cap the income value at a level that keeps that intact.
3. Assign a new value.
If an outlier seems to be due to a mistake in your data, you try imputing a value. Common imputation methods include using the mean of a variable or utilizing a regression model to predict the missing value.
4. Try a transformation.
A different approach to true outliers could be to try creating a transformation of the data rather than using the data itself. For example, try creating a percentile version of your original field and working with that new field instead.
Just how much an outlier affects your analysis depends, not surprisingly, on a few factors. One factor is dataset size. In a large dataset, each individual point carries less weight, so an outlier is less worrisome than the same data point would be in a smaller dataset. Another consideration is “how much” of an outlier a point might be – just how far out of line with the rest of your dataset a single point is. A point that is ten times as large as your upper boundary will do more damage than a point that is twice as large.
These are a few ways that we’ve found to help with outliers, but there are certainly others. I’d love to know – what has your experience been with outliers? Do you use any of the above methods?
-Caitlin Garrett, Statistical Analyst
https://conversionxl.com/blog/outliers/
One thing many people forget when dealing with data: outliers.
Even in a controlled online a/b test experiment, your dataset may be skewed by extremities. How do you deal with them? Trim them out, or is there some other way?
How do you even detect the presence of outliers and how extreme they are?
Especially if you’re optimizing your site for revenue, you should care about outliers. This post will dive into the nature of outliers in general, how to detect them, and then some popular methods for dealing with them.
What Are Outliers?
First, what exactly are outliers?
An outlier is an observation that lies an abnormal distance from other values in a random sample from a population.
There is, of course, a degree of ambiguity here. Qualifying a data point as an anomaly leaves it up to the analyst or model to determine what is actually abnormal and what to do with such data points.
There are also different degrees of outliers:
- Mild outliers lie beyond an inner fence on either side
- Extreme outliers are beyond an outer fence
Why do outliers occur? According to Tom Bodenberg, chief economist and data consultant at market research firm Unity Marketing, “It can be the result of measurement or recording errors, or the unintended and truthful outcome resulting from the set’s definition.”
Outliers could contain valuable information, they could be meaningless aberrations caused by measurement and recording errors, they could cause problems with repeatable A/B test results. So it’s important to question and analyze outliers in any case to see what their actual meaning is.
Why are they occurring, where, and what might the meaning be? The answer could be different business to business, but it’s important to have the conversation rather than to ignore the data regardless of the significance.
The real question, though, is how do outliers affect your testing efforts?
How Outliers Affect A/B Testing
Though outliers will show up in many analysis situations, for the sake of conversion optimization, you should mostly be concern about tests where you’re optimizing for revenue metrics like Average Order Value or Revenue Per Visitor.
You can easily imagine anecdotally how outliers could affect a single A/B test result. If not, here’s Taylor Wilson, Senior Optimization Analyst at *s Bell, explaining a few scenarios in which that could happen:

“In this particular situation, resellers were the culprit—customers who buy in bulk with the intention of reselling items later. Far from your typical customer, they place unusually large orders, paying little attention to the experience they’re in.
It’s not just resellers who won’t be truly affected by your tests. Depending on your industry, it could be very loyal customers, in-store employees who order off the site, or another group that exhibits out-of-the-ordinary behavior.”
Especially in data sets with low sample sizes, outliers can mess up your whole day.
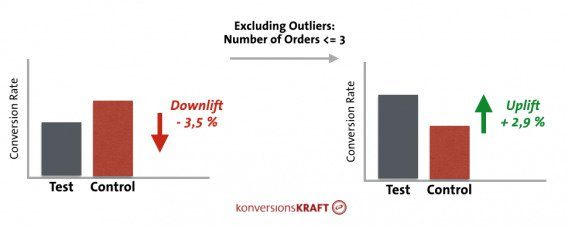
As Dr. Julia Engelmann, Head of Data Analytics at Konversionkraft, mentioned in a CXL blog post, “Almost every online shop has them and usually they cause problems for the valid evaluation of a test: the bulk orderers.”
So this isn’t a rare, fringe problem. She shared this specific example of how including and excluding outliers can affect the results of a test, and ultimately the decision you make:
A problem outliers can cause in A/B tests, HiConversion noted, is that outliers tend not to be affected by the smaller UI changes that may affect a more fickle and mainstream population. Bulk orderers will push through your smaller usability changes like your average visitor may not.
Their article outlined a case where outliers skewed the results of a test. Upon further analysis, the outlier segment was 75% return visitors and much more engaged than the average visitor.
Think your data is immune to outliers? Maybe it is, but probably not – and in any case, it’s best to know for sure. So how do you diagnosis that on your own? That is to say, how do you detect outliers in your data?
How to Detect Outliers in Data
Data visualization is a core discipline for analysts and optimizers, not just to better communicate results with executives, but to explore the data more fully.
As such, outliers are often detected through graphical means, though you can also do so by a variety of statistical methods using your favorite tool (Excel and R will be referenced heavily here, though SAS, Python, etc. all work).
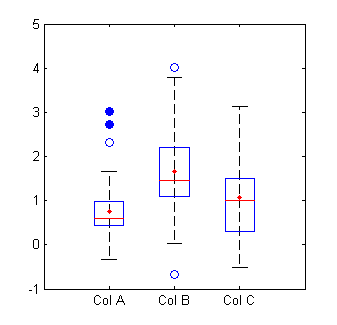
Two of the most common graphical ways of detecting outliers are the boxplot and the scatterplot. A boxplot is my favorite way.
You can see here that the blue circles are outliers, with the open circles representing mild outliers and closed circles representing extreme outliers:
It’s really easy to analyze boxplots in R. Just use boxplot(x, horizontal = TRUE) where x is your data set to make something that looks like this:
Even better, you can use boxplot.stats(x) function, where x is your data set, to get summary stats that includes the list of outliers ($out):
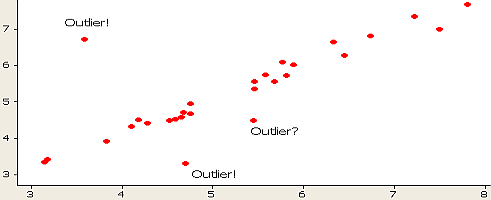
You can also see these in a scatterplot, though I believe it’s a bit harder to tell with clarity what extreme and mild outliers are:
A histogram can work as well:
You can also see outliers fairly easily in run charts, lag plots (a type of scatterplot), and line charts, depending on what type of data you’re working with.
Conversion expert Andrew Anderson also backs the value of graphs to determine the effect of outliers on data:

“The graph is your friend. One of the reasons that I look for 7 days of consistent data is that it allows for normalization against non normal actions, be it size or external influence.
The other thing is that if there are obvious non-normal action values, it is ok to normalize them to the average as long as it is done unilaterally and is done to not bias results. This is only done if it is obviously out of normal line and usually I will still run the test another 2-3 extra days just to make sure.”
As to the latter point on non-normal distributions, we’ll go into that a bit later in the article.
But is there a statistical way of detecting outliers, apart from just eyeballing it on a chart? Indeed, there are many ways to do so (outlined here), the main two being a standard deviation approach or Tukey’s method.
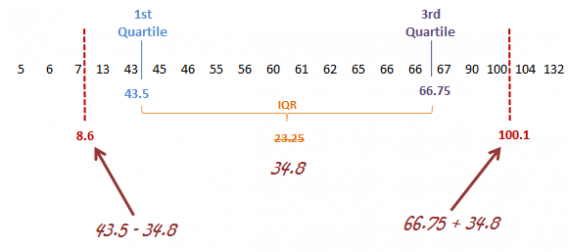
In the latter, extreme outliers tend to lie more than 3.0 times the interquartile range below the first quartile or above the third quartile, and mild outliers lie between 1.5 times and 3.0 times the interquartile range below the first quartile or above the third quartile.
It’s pretty easy to highlight outliers in Excel. While there’s no built-in function for outlier detection, you can find the quartile values and go from there. Here’s a quick guide if you’re interested in doing that.
Strategies for Dealing with Outliers in Data
Should an outlier be removed from analysis? The answer, though seemingly straightforward, isn’t so simple.
There are many strategies for dealing with outliers in data, and depending on the situation and data set, any could be the right or the wrong way. In addition, most major testing testing tools have strategies for dealing with outliers, but they usually differ in how exactly they do so.
Because of that, it’s still important to do your own custom analysis with regards to outliers, even if your testing tool has its own default parameters. Not only can you trust your testing data better, but sometimes analysis of outliers produces its own insights that will help with optimization.
So let’s go over some common strategies:
Set Up a Filter in Your Testing Tool
Even though this has a little cost, filtering out outliers is worth doing it because you can often discover significant effects that are simply “hidden” by outliers.
According to Himanshu Sharma at OptimizeSmart, if you are tracking revenue as a goal in your A/B testing tool, you should set up a code which filters out abnormally large orders from your test results.
He says that you should look at your past analytics data to secure an average web order, and to set up filters with that in mind. In his example, imagine you have that your website average order value in the last 3 months has been $150 – then any order which is above $200 can be considered as an outlier.
Then it’s all about writing a bit of code to stop the tool from passing that value. Here are some brief instructions on how to do that in Optimizely. The tl;dr is that you exclude values above a certain amount with code that looks something like this (for orders above $200):
if(priceInCents <20000){
window.optimizely = window.optimizely || [];
window.optimizely.push([‘trackEvent’,
‘orderComplete’, {‘revenue’: priceInCents}]);
Remove or Change Outliers During Post-Test Analysis
Kevin Hillstrom, President of Mine That Data, explained why he will sometimes adjust outliers in tests…

“On average, what a customer spends is not normally distributed.
If you have an average order value of $100, most of your customers are spending $70, $80, $90, or $100, and you have a small number of customers spending $200, $300, $800, $1600, and one customer spending $29,000. If you have 29,000 people in the test panel, and one person spends $29,000, that’s $1 per person in the test.
That’s how much that one order skews things.”
One way to account for this is simply to remove outliers, or trim your data set as to exclude as many as you’d like.
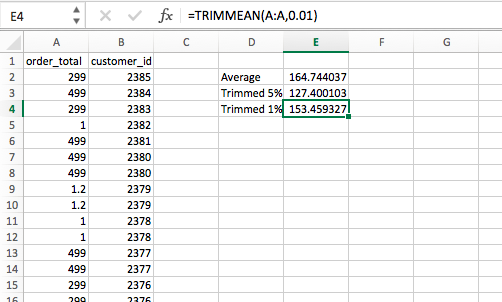
This is really easy to do in Excel – a simple TRIMMEAN function will do the trick. The first argument is the array you’d like to manipulate (column A here), and the second argument is by how much you’d like to trim the upper and lower extremities:
Trimming values in R is super easy, too. It exists within the mean(function). So, say you have a mean that differs quite a bit from the median, it probably means you have some very large or small values skewing it. In that case, you can trim off a certain percentage of the data on both the large and small side. In R, it’s just mean(x, trim = .05), where x is your data set and .05 can be any number of your choosing:
This process of using Trimmed Estimators is usually done to obtain a more robust statistic. By the way, the median is the most trimmed statistic, at 50% on both sides (which you can also do with the mean function in R – mean(x, trim = .5)).
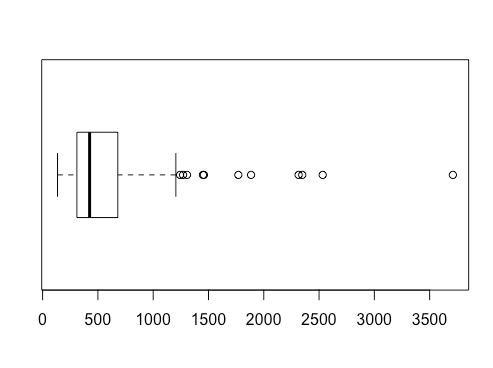
Most of the time in optimization, your outliers will be on the higher end because of bulk orderers. Given your knowledge of historical data, if you’d like to do a post-hoc trimming of values above a certain parameter, that’s very easy to do in R. If the name of my data set is “rivers” I can do this, given the knowledge that my data usually falls under 1210: rivers.low <- rivers[rivers<1210].
That creates a new variable only consisting of what I deem to be non-outlier values, and from there I can boxplot it, getting something like this:
Clearly there are fewer outlier values, though there are still a few. This will virtually always happen, no matter how many values you trim from the extremes.
You can also do this by removing values that are beyond three standard deviations from the mean. To do that, first you need to extract the raw data from your testing tool. Optimizely reserves this ability for their enterprise customers unless you ask support to help you.
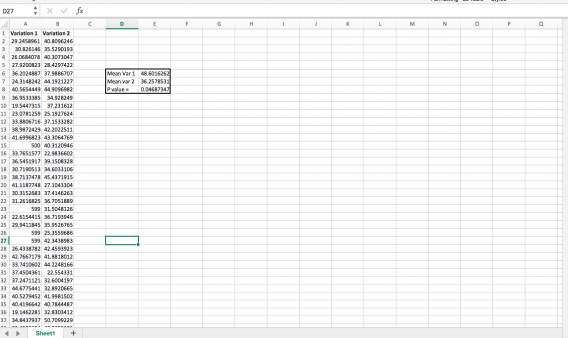
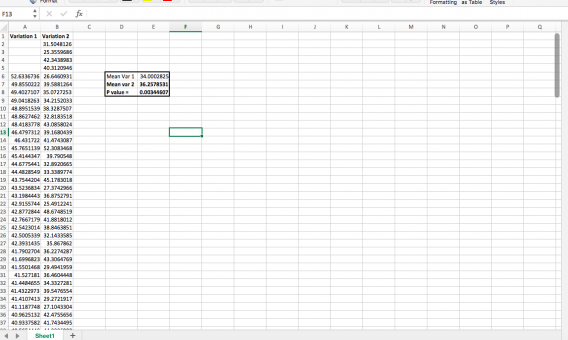
Instead of taking real client data, just to demonstrate how to do this, I generated two random sequence of numbers with normal distributions (using =NORMINV(RAND(),C1,D1) where C1 is mean and D1 is SD, for reference). In “variation 1,” though, I added a few very high outliers, making variation 1 a “statistically significant” winner:
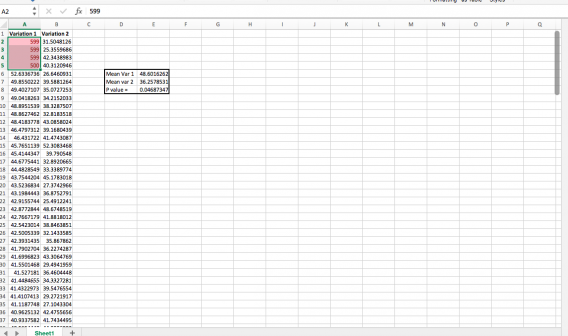
Then you can use conditional formatting to highlight those that are above 3 standard deviations. Chop those off:
And you have a different statistically significant winner:
My example is incredibly clean cut and probably simpler than you’ll deal with, but at least you can see how just a few very high values can throw things off (and one possible solution to that). If you want to play around with outliers using this fake data, click here to download the spreadsheet.
Change the Value of Outliers
Much of the debate on how to deal with outliers in data comes down to the following questions: should you keep outliers, remove them, or change them to another variable?
Essentially, instead of simply removing the outliers from the data, in this case you take your set of outliers and change their values to something more representative of your data set. It’s a small distinction, but important: when you trim data, the extreme values are discarded. When you use winsorized estimators (changing the values), extreme values are instead replaced by certain percentiles (the trimmed minimum and maximum).
Kevin Hillstrom mentioned in his podcast that he trims the top 5% or top 1% (depending on the business) of orders and changes the value (e.g. $29,000 to $800). As he says, “You are allowed to adjust outliers.”
Consider the Underlying Distribution
Traditional methods to calculate confidence intervals assume that the data follows a normal distribution, but as we discussed above, with certain metrics like average revenue per visitor, that usually isn’t the way reality works.
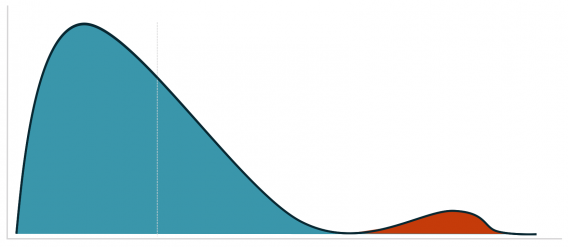
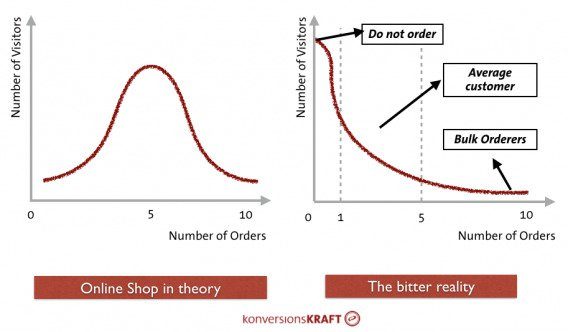
In another section of Dr. Julia Engelmann’s wonderful article for our blog, she shared a graphic depicting this difference. The left graphic shows a perfect (theoretical) normal distribution. The number of orders fluctuates around a positive average value. In the example, most customers order five times. More or fewer orders arise less often.
The graphic to the right shows the bitter reality. Assuming an average conversion rate of 5%, 95% are customers who don’t buy. Most buyers have probably placed one or two orders, and there are a few customers who order an extreme quantity.
The distribution on the right side is known as a “right-skewed” distribution.
Essentially, the problem comes in when we assume that a distribution is normal but we’re actually working with something like a right skewed distribution. Confidence intervals can no longer be reliably calculated.
With your average ecommerce site, let’s say at least 90% of customers will not buy anything. Therefore, the proportion of “zeros” in the data is extreme and the deviations in general are enormous, including extremities because of bulk orders.
In this case, it’s worth taking a look at the data using other methods than the t-test. (The Shapiro-Wilk test lets you test your data for normal distribution, by the way). All of these were suggested in this article:
1. Mann-Whitney U-Test
The Mann-Whitney U-Test is an alternative to the t-test when the data deviates greatly from the normal distribution.
2. Robust statistics
Methods from robust statistics are used when the data is not normally distributed or distorted by outliers. Here, average values and variances are calculated such that they are not influenced by unusually high or low values – which I sort of went into with windsorization above.
3. Bootstrapping
This so-called non-parametric procedure works independently of any distribution assumption and provides reliable estimates for confidence levels and intervals. At its core, it belongs to the resampling methods. They provide reliable estimates of the distribution of variables on the basis of the observed data through random sampling procedures.
Consider the Value of Mild Outliers
As mentioned, with Revenue Per Visitor the underlying distribution is often non-normal. It’s common for few big buyers to skew the data set towards the extremes. When this is the case, outlier detection falls prey to predictable inaccuracies – it detects outliers far more often.
So there’s a chance that in your data analysis, you shouldn’t throw away outliers. Rather, you should segment them and analyze them deeper. What demographic, behavioral, firmographic traits correlate with their purchasing behavior and how can you run an experiment to tease out some causality there?
This is a question that runs deeper than simple A/B testing and is core to your customer acquisition, targeting, and segmentation efforts. I don’t want to go too deep here, but I want to say that for various marketing reasons, analyzing your highest value cohorts can bring profound insights as well.
No Matter What, Do Something
In any case, it helps to have a plan in place. As Dan Begley-Groth wrote on the Richrelevance blog:

“In order for a test to be statistically valid, all rules of the testing game should be determined before the test begins. Otherwise, we potentially expose ourselves to a whirlpool of subjectivity mid-test.
Should a $500 order only count if it was directly driven by attributable recommendations? Should all $500+ orders count if there are an equal number on both sides? What if a side is still losing after including its $500+ orders? Can they be included then?
By defining outlier thresholds prior to the test (for RichRelevance tests, three standard deviations from the mean) and establishing a methodology that removes them, both the random noise and subjectivity of A/B test interpretation is significantly reduced. This is key to minimizing headaches while managing A/B tests”
Whether you believe outliers don’t have a strong effect on your data and choose to leave them as is, or whether you want to trim the top and bottom 25% of your data, the important thing is that you’ve thought it through and have an active strategy. Being data-driven means considering anomalies like this, and to ignore them means you could be making decisions on faulty data.
Conclusion
Outliers are something not discussed often in testing, but depending on your business and what metric you’re optimizing, they could certainly be affecting your results.
As we’ve seen, one or two high values in a smaller sample size can totally skew a test, leading you to make a decision off of faulty data. No bueno.
For the most part, if your data is affected by these extreme cases, you can bound the input to a historical representative of your data that excludes outliers. So that could be a number of items (>3) or a lower or upper bounds on your order value.
Another way, perhaps better in the long run, would be to export your post-test data and visualize it by various means. Determine on a case-by-case basis what the effect of the outliers was. And from there, decide whether you want to remove, change, or keep the outlier values.
Really, though, there are lots of ways to deal with outliers in data. It’s not a simple quick fix that works across the board, and that’s why the demand for good analysts continues to grow.