一、明确功能需求
- 项目功能需求如下图所示,假设有1000行数据即1000名患者,已知每名患者的西医指标值和医生给出的证候结果。
- 共有3个证候结果:气虚证、肾虚证、阳虚证,列序号分别为1、2、3列;值为1表示患者存在该证候,值为0表示不存在该证候,一个患者可以同时存在多个证候,证候起始和终止序号为2-4。
- 共有12个西医指标:白细胞、红细胞、血红蛋白等,列序号分别为4、5、6...,指标值为浮点数值。西医指标起始和终止序号为5-16。
- 需求:对所有数据,考虑每个证候,计算出存在证候和不存在该证候的两组数据,首先判断这些数据是否属于正态分布,正态分布是用Ttest检验,非正态分布时用非参数Kruskal-Wallis检验,然后对比该两组数据的均值、标准差、检验t值、p值,从而分析出西医指标对存在该证候的影响、相关性。
每个证候输出一个结果文件,文件中显示所有西医指标的计算结果值,按照p值从小到大排序,前几个指标即是对该证候影响较大的指标。以气虚证和非气虚证为例,检验两组数据有无差异性,通过均值和标准差可以看出来气虚和非气虚的指标的高低,
通过p值可以看出有无统计学意义,若p<0.05差异显著,否则差异不显著;通过p值最小的几个指标,可以看出这些指标对于判断是否属于气虚证候的影响。
可使用任何语言解决,我们前期介绍了使用java解决,设计了算法框架。这里使用python实现,python解决时代码更为简洁,也更简单。
二、设计算法
充分理解需求的情况下,设计算法框架。
要求遍历所有证候,,每个证候单独输出一个文件; 在这个文件中, 对所有西医指标进行考虑,即遍历所有西医指标;
对于每个西医指标,要考虑所有行的记录(即遍历所有行), 分别计算证候为0和为1时的西医指标值。
通过上述分析,整体的算法框架需要三层循环, 第一层为遍历每个证候, 第二层为遍历每个西医指标, 第三层为遍历每行记录,伪代码如下:
> For 证候 synIndex 1:6 //假设有6个证候
> 创建证候文件, 待输出数据
> For 西医指标med 7:56 //假设有50个西医指标
> 创建动态数组, 存储指标值以及证候值
> For 每行记录row
> 将西医指标值,根据证候值分别加入不同的动态数组
> End 每行记录row
> 依据数组中的值, 计算p值、t值、均值等等.
> 将该指标名称、p值、t值等信息作为一行,追加写入文件.
> End 西医指标med
> 关闭csv文件,考虑下一个证候
> End For 证候
三、设计细节
3.1 分组存储西医指标值,由于证候0和1的个数不确定, 所以它们数组大小也不确定,
需要使用动态数组分别存储证候0和1对应的西医指标值,可采用ist等数据结构来创建动态数组,用于存储西医指标值。
3.2 读入及操作xls文件,采用 pandas 读取xls文件数据,tcm_data =
pd.read_excel('data_expert.xls'), 读取出所有列名measures =
tcm_data.columns.values.tolist()。并按照算法来操作数据,进行运算处理。
3.3 使用stats.ttest_ind函数来进行Ttest检验,test_res = stats.ttest_ind(group2, group1,
equal_var =
False),group2为证候为1的指标组,group1为证候为0的指标组;test_res[1]值为返回p值,test_res[0]为返回t值。
3.4 使用 kruskalwallis函数进行非参数检验, h, p = kruskalwallis(group2,
group1),group2和group1的含义同上,返回的p值既是结果p值。
3.5 使用stats.normaltest函数进行判断是否属于正态分布,p1 =
stats.normaltest(groupAll),groupAll是group1和group2的合并.
若返回值p1>0.003,即为正态分布,若p1<0.003,则为非正态分布。
3.6 使用save = pd.DataFrame(final_table)
save.to_csv(OneCsvName,float_format='%.3f',na_rep="NAN!", header=False
),输出结果文件csv格式。
西医指标值存在为空情况,当空值的个数大于数据条数的一半时,不再进行计算处理,设特殊标记表示。
总体算法框架如下图所示
四、编制代码
依据上述分析,按照算法框架,使用python编制代码,其中核心的实现代码如下
4.1 首先读取文件数据和列名称,初始化证候范围和西医指标范围
tcm_data = pd.read_excel('data_expert.xls')
measures = tcm_data.columns.values.tolist()
wid_s = 5 #5
wid_e = 16 #16
the index range of Chinese medicine diagnosis
cid_s = 2 #1
cid_e = 4 #8
数据文件与源码文件在同一目录下。
4.2 我们把写出文件、考虑某证候把该证候值传递出去, tmp_data来接受返回的结果;他们
单独放在一个函数中,函数名为output_result_csv(),代码如下
def output_result_csv():
'''
For Chinese medicine diagnosis rules, save the relevant results in a file,
output a csv file for one rules.
Meanwhile, it can output many csv files based on measures for one rule
'''
for cid in range(cid_s, cid_e+1): #2,3,4
for cid in range(2, 4): #2,3,4
tmp_data = contrast_test(cid)
tmp_ids = tmp_data['top_ids']
tmp_samples_size = tmp_data['top_samples_size']
tmp_means = tmp_data['top_means']
tmp_variances = tmp_data['top_variances']
tmp_normality = tmp_data['top_normality']
tmp_scores = tmp_data['top_scores']
tmp_scorest = tmp_data['top_scorest']
wes_measures = []
for t in tmp_ids:
wid = t + wid_s
wes_measures.append(measures[wid])
t_scores = tmp_scorest
p_scores = tmp_scores
class_west_m = class_west_measures(wes_measures) #call function to gieve
measure's class
tableold = [class_west_m, wes_measures, tmp_means[:,1], tmp_variances[:,1], \
tmp_means[:,0], tmp_variances[:,0],tmp_normality, p_scores]
np_table = np.array(tableold) #change to numpy type
np_tableT = np_table.T#change T
rowname = ('西医指标类别','西医指标','此证候人群均值','此证候人群方差',\
'非此证候人群均值','非此证候人群方差','是否正态分布', 'p值')#add the row name
final_table = np.row_stack((rowname, np_tableT))
different name of csv file, one rule of Zheng save a csv file, the csv file
contain all west measures
OneCsvName = measures[cid] + '.csv';
save = pd.DataFrame(final_table)
save.to_csv(OneCsvName,float_format='%.3f',na_rep="NAN!", header=False )
4.3 我们把对某个证候的具体计算处理,单独放在一个函数中,即4.2中的contrast_test()函数,如下
def contrast_test(cid):
'''
- Use the Chinese medicine diagnosis rules to partition the patients into two groups;
- Test whether the values measured by modern western medicine have significant differences
betwen the two group patients; - Use student's t-test score, for simplicity, assume Gaussian distribution, independent two sample sets,
unequal sample size, and unequal variance.
--- input cid: the index of a Chinese medicine diagnosis rule
--- return the top 5 colost relevant western biomedical measurements and the means, variances, as well as the t-test values.
'''
name = measures[cid]
lables = tcm_data[name].values.tolist()
wid_size = wid_e - wid_s + 1
means = np.zeros((wid_size,2))
variances = np.zeros((wid_size,2))
normality = np.zeros(wid_size) # save normality or not. 1 means normality,0
means not normality
scores = np.zeros(wid_size) #save p
scorest = np.zeros(wid_size)#save t
cnt = 0
samples = list()
samples_size = list()
for j in range(wid_s, wid_e + 1):
bio_measures = tcm_data[measures[j]].values.tolist()
n1 = 0
n2 = 0
x1 = 0
x2 = 0
s1 = 0
s2 = 0
group1 = list()
group2 = list()
for i in range(len(lables)):
if not np.isnan(bio_measures[i]):
if lables[i] == 0:
n1 += 1
x1 += bio_measures[i]
group1.append(bio_measures[i])
if lables[i] == 1:
n2 += 1
x2 += bio_measures[i]
group2.append(bio_measures[i])
tmp_sample = {'group1':group1, 'group2':group2}
samples.append(tmp_sample)
samples_size.append([n1, n2])
if the number of missing value > 50%, do not consider this medical measure
if (n1 + n2) <= (0.5 * len(lables)):
scores[cnt] = 100
cnt += 1
continue
x1 /= n1
x2 /= n2
for i in range(len(lables)):
if not np.isnan(bio_measures[i]):
if lables[i] == 0:
s1 += (bio_measures[i] - x1) ** 2
if lables[i] == 1:
s2 += (bio_measures[i] - x2) ** 2
means[cnt, 0] = x1 #存储证候为0时的指标均值
means[cnt, 1] = x2 #存储证候为1时的指标均值
variances[cnt, 0] = np.sqrt(s1 / (n1 - 1)) #存储证候为0时的指标方差
variances[cnt, 1] = np.sqrt(s2 / (n2 - 1)) #存储证候为1时的指标方差
normality[cnt] = normality_or_not(group2, group1)
if normality[cnt] == 1: #正态分布,使用Ttest检验
perform Welch’s t-test
test_res = stats.ttest_ind(group2, group1, equal_var = False)
scores[cnt] = test_res[1] # save p, the smaller, the more significant
scorest[cnt] = "%.2f" % test_res[0] #save t, the bigger of abs(t), the more
significant
else: #非正态分布,使用非参数检验Kruskal-Wallis
h, p = kruskalwallis(group2, group1)
scores[cnt] = p
cnt += 1
samples = np.asarray(samples)
samples_size = np.asarray(samples_size)
''' Note that the next two lines is very important
top_ids = np.argsort(scores)[0:top_k] #Sorted operation by value of p to find
top_k measurements, return the index of value
top_ids = np.arange(0,len(scores),1) #Don't sort by value of p
'''
find the top k relevant measurements according p
top_k = wid_size #find all the measurements, you can change this value to any
number you need
top_ids = np.argsort(scores)[0:top_k] #sort operation by value of p, return
the index of value, if you need sort, use this line and don't use next line
top_ids = np.arange(0,len(scores),1) #Don't sort by value of p,return the
original index of value.
top_means = means[top_ids,:]
top_variances = variances[top_ids,:]
top_normality = normality[top_ids]
top_scores = scores[top_ids]#p
top_scorest = scorest[top_ids]#t
top_samples = samples[top_ids]
top_samples_size = samples_size[top_ids]
return the results
data_infos = {"cid":cid, "top_ids":top_ids,
"top_samples_size":top_samples_size,"top_means":top_means,
"top_variances":top_variances, "top_normality":top_normality,
"top_scores":top_scores, "top_samples":top_samples, "top_scorest":top_scorest}
return data_infos
4.4 我们使用 normality_or_not()函数来判断是否为正态分布,正态返回1,非正态返回0;函数如下
def normality_or_not(group2, group1):
'''
如果两组数据合并一起,若是正态分布,则返回1,后期使用Ttest检验;否则返回0,后期使用非参数检验
'''
若p>0.003,即为正态分布
若p<0.003,则为非正态分布
groupAll = list(group1)
groupAll.extend(group2)
p1 = stats.normaltest(groupAll)
p2 = stats.normaltest(group2)
if(p1[1]>0.003): #and (p2[1]>0.003)):
normality = 1
else:
normality = 0
return normality
五、简单测试
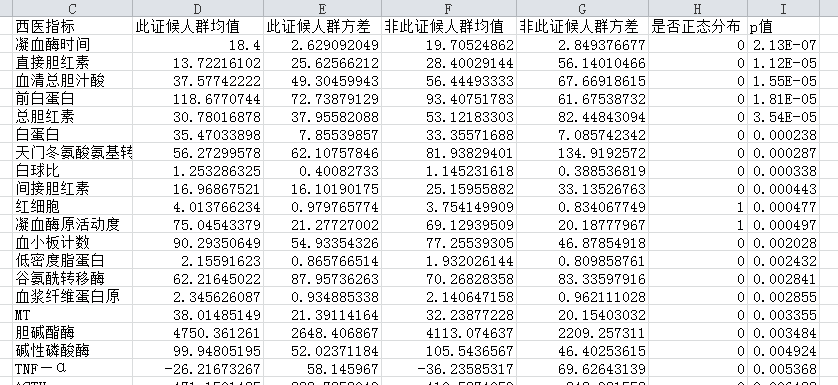
结果如下图所示,假设该证候为气虚证,结果显示出了有气虚证和无气虚证,他们之间西医指标的差别,以及指标对证候的影响,还可以看出,西医指标值大部分都不服从正态分布,凝血酶时间、直接胆红素、血清总胆汁这些指标对证候的影响明显。
六、结论
** 特别声明: **
** 上述教程源于实际的项目案例,在发布时对这些实验数据进行了处理改造。 **
**
**
**
该教程版权归河南中医药大学信息技术学院、香港科技大学计算机系、北京中医药大学共同所有,仅供于免费学习和交流,特别为河南中医药大学计算机文化基础课,python程序设计提供教学辅助。
**
**
**
** 转载请注明出处,若用于商业用途,版权所有者将保留追究法律权利。 **