《信用评分卡模型分数校准》

2024-01-01 16:23:46

信用评分卡模型分数校准

风控业务背景

在评分卡建模中，我们通常会把LR输出的概率分（probability）转换为整数分(score)，称之为评分卡分数校准(calibration)。事实上，这个阶段称为尺度变换（scaling）或许更为合适。只是有些书中并不严格区分校准和尺度变换，统称为风险校准。

大家耳熟能详的一些信用评分就是最终以这种形式呈现，例如：

1. 芝麻分的分值范围为350～950，分值越高代表信用越好，相应违约率相对较低，较高的芝麻分可以帮助用户获得更高效、更优质的服务。（摘自：芝麻信用官网）
2. FICO分的分值范围为300～850，分数越高, 说明客户的信用风险越小。

但我们可能并不清楚这些问题：分数校准的概念是什么？为什么要做分数校准？分数校准的原理是什么？如何做分数校准？在哪些场景里需要做分数校准？

目前鲜有资料系统讲述这些问题，本文希望针对这一命题给出一套相对完整的理论。

目录
Part 1. 分数校准的概念
Part 2. 分数校准的业务应用场景
Part 3. 如何进行概率分数校准？
Part 4. 如何定量评估校准的好坏？
Part 5. 概率分数尺度变换成整数分数
Part 6. 总结
致谢
版权声明
参考资料

Part 1. 分数校准的概念

在机器学习模型实践应用中，大多数情况下，我们主要关注分类模型的排序性（ranking），而很少关心输出概率的具体数值。也就是——关注相对值，忽略绝对值。

一方面，有的分类器（例如SVM）只能直接打上类别标签没法给出置信度。另一方面，在某些场景中，我们希望得到真实的概率。例如，在信贷风控中，将预测的客户违约概率(Probability of Default ，PD）与真实违约概率对标，即模型风险概率能够代表真实的风险等级。这样我们就可以进行更准确的风险定价。

这就引出了校准(calibration)的概念，我们将其理解为：

预测分布和真实分布（观测）在统计上的一致性。

对于完美校准的（2分类）分类器，如果分类器预测某个样本属于正类的概率是0.8，那么就应当说明有80%的把握（置信度，confidence level）认为该样本属于正类，或者100个概率为0.8的样本里面有80个确实属于正类。

由于我们无法获知真实的条件概率，通常用观测样本的标签来统计代替，并用可靠性曲线图（Reliability Curve Diagrams）来直观展示当前模型的输出结果与真实结果有多大偏差。如图1所示，如果数据点几乎都落在对角线上，那么说明模型被校准得很好；反之，如果和对角线的偏离程度越明显，则校准越差。

图 1 - 校准曲线（横坐标 = 预测概率，纵坐标 = 实际频率）

Reliability diagrams (Hartmann et al. 2002) are simply graphs of the Observed frequency of an event plotted against the Forecast probability of an event.
This effectively tells the user how often (as a percentage) a forecast probability actually occurred.

因此，其横坐标为事件发生预测概率，纵坐标为事件发生实际频率，能展示“某个事件预测概率 VS 实际发生的频率“之间的关系。对于一个理想的预测系统，两者是完全一致的，也就是对角线。

那么可靠性曲线图是如何绘制的？步骤如下：

step 1. 横坐标：将预测概率升序排列，选定一个阈值，此时[0，阈值]作为一个箱子。
step 2. 纵坐标：计算这个箱子内的命中率（hit rate），也就是正样本率。
step 3. 选定多个阈值，重复计算得到多个点，连接成线。

$hit\_rate = \frac{positive}{positive+negative} \tag{1}$

我们以扔硬币来评估正面朝上的概率这个场景进行说明。经过投掷记录，我们得到1W（或者更多）个有真实0（反面朝上）和1（正面朝上）标签的样本。进而，我们根据硬币的各类特征和正反面标签，训练得到一个二分类模型，给这批样本打上分，升序排列。然后，取一个分数作为阈值（如0.5），统计分数取值为0～0.5的这批样本中1的实际占比，当作“真实”概率。最后，比较“真实”概率与预测概率来检测一致性。

在实践中，我们已经普遍认识到一个现象：

LR的输出概率可以认为是真实概率，而其他分类器的输出概率并不反映真实概率。

那么这背后的数学原理是什么？

Part 2. 分数校准的业务应用场景

分数校准主要目的在于：

ensure that the scores provided by different scorecards have the same meaning.
确保不同评分卡给出的分数具有相同的含义。
determine or refine the probability estimates to be associated with each score, converted into the actual rate of the outcome (default)
保证预测概率与真实概率之间的一致性（拟合度）。
modifying for the difference between the expected rate based on the historical database and the actual rate observed.
修正实际概率和开发样本中期望概率之间的偏差。

接下来，我们将结合实际业务场景展开介绍。注意，因为我们是用评分卡(LR)建立的模型，因此分数校准实际只做了尺度变换这一步。

场景1: 分群评分卡

有时候我们会发现单一评分卡在全量人群上表现并不是特别好。此时会采用先分群（segmentation），再针对各人群建立多个子评分卡模型。

基于以下几个原因，我们需要把分数校准到同一尺度。

针对多个分支模型需要制订多套风控策略，将会大大增加策略同学的工作量，且不利于策略维护调整。
不同评分卡输出的分数并不具有可比性，它们的分布存在差异。为了融合后统一输出一个最终分数。
各分群评分卡相当于一个分段函数，分数之间存在跃变。校准可以保证各分数具有连续性。

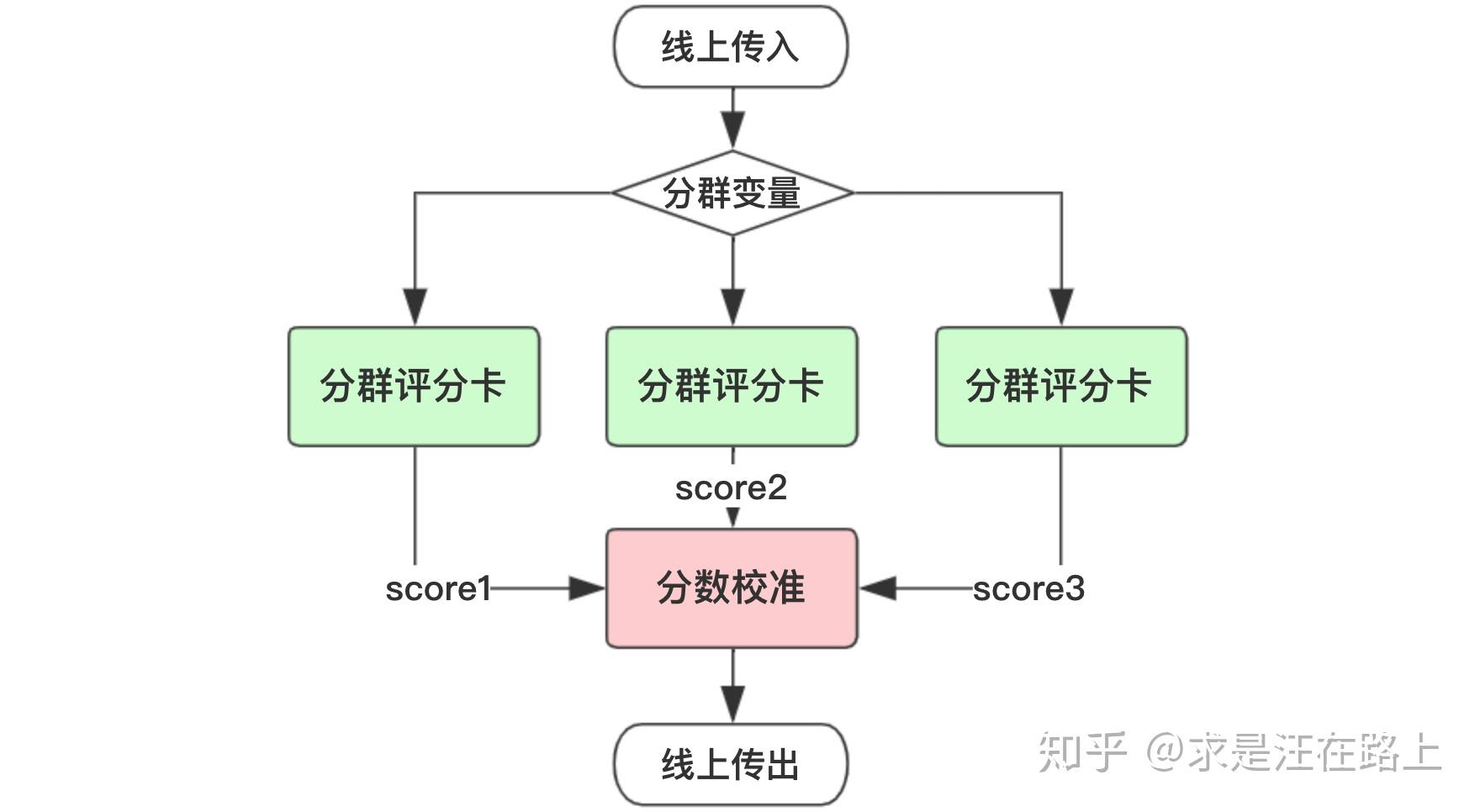图 2 - 分群评分卡场景

场景2: 降级备用策略

在用到外部数据建模时，考虑到外部数据采集上存在潜在的不稳定性，我们通常会采取降级策略。也就是说，去掉外部数据后再建立一个模型，作为主用（active）模型的一个备用（standby）模型。如果外部数据有一天停止提供服务，就可以切换到备用模型上。

同时，为了使下游业务调用无感知，我们会将主用备用模型的分数校准至一个尺度。这样就能保证风控策略同学只需要制订一套cutoff方案，且不用调整，只需做必要的策略切换日志和前后波动监控即可。

图 3 - 降级备用策略

场景3: 客群变化修正

当面向客群发生变化时，开发样本与最近样本之间存在偏差（bias）。如果开发样本的Odds大于实际的Odds，那么计算每个分数段的坏样本率，得出来的结果将会大于真实情况。

然而考虑到建模成本，我们有时并不想refit模型，此时就可以利用最近样本对评分卡进行校准，修正偏差。

图 4 - 基于近期样本校准

Part 3. 如何进行概率分数校准？

针对上述实际业务场景，我们该如何去做概率分数校准呢？以下是两种最为常见的概率校准方法：

Platt scaling使用LR模型对模型输出的值做拟合（并不是对reliability diagram中的数据做拟合），适用于样本量少的情形，如信贷风控场景中。
Isotonic regression则是对reliability diagram中的数据做拟合，适用于样本量多的情形。例如搜索推荐场景。样本量少时，使用isotonic regression容易过拟合。

现以数值案例展示前文中的三个场景。

方案1：针对场景1和2的Platt校准

假设目前有一个LR模型分数score1，并令score2 = 0.75*score1，以此来模拟场景1和2。此时score1和score2的排序性完全一致，只是绝对值不同，对应不同的风险等级，如图5所示。我们需要将score1和score2校准到同一尺度。

图 5 - 两个分支模型的概率分布

普拉托（Platt）最早提出可以通过sigmoid函数将SVM的预测结果转化为一个后验概率值，其实施流程为：

step 1. 利用样本特征X和目标变量y训练一个分类器model1。（不限定分类器类型）
step 2. 利用model1对样本预测，得到预测结果out。
step 3. 将预测结果out作为新的特征X'，再利用样本的标签y，训练一个LR。
step 4. LR最后输出的概率值就是platt's scaling后的预测概率。

我们把score1和score2分别执行step 3，得到校准后的分数score1_cal和score2_cal，如图6所示。通过分布可知，两个分数的差异几乎为0，故而具有相同的风险等级。同时，由于校准函数是单调的，那么校准前后将不会影响排序性和区分度。

图 6 - 校准后的两个分支模型的概率分布

方案2：针对场景3的Odds校准

场景3一般称为评分卡分数的错误分配（Misassignment），如图7所示。

图 7 - 截距错配(Intercept Misalignment)

我们知道，LR中的截距近似于开发样本的ln(Odds)，那么就可以采取以下方式进行校准。

$\left\{ \begin{aligned} ln(\frac{p}{1-p}) = w * x + ln({Odds_{expect}}) \\ ln({Odds_{calibrate}}) = ln(\frac{Odds_{actual}}{Odds_{expect}}) = ln(Odds_{actual}) - ln({Odds_{expect}})\\ \end{aligned} \right. \\ \Rightarrow ln(\frac{p}{1-p}) = w_1 * x_1 + ln({Odds_{expect}}) + ln({Odds_{calibrate}}) \\ \Rightarrow ln(\frac{p}{1-p}) = w_1 * x_1 + ln({Odds_{actual}}) \tag{1}$

在评分卡尺度变换后，我们可以得到ln(Odds)和Score之间的线性关系（后文会介绍），也就是：

$Score = A - B * Ln(Odds) \tag{2}$

那么，利用近期样本和开发样本就可以分别绘制出这样一条直线。如果这两条直线是平行关系，此时我们认为：在同一个分数段上，开发样本相对于近期样本把Odds预估得过大或过小。因此，可通过 $Ln(Odds_{actual}) - Ln(Odds_{expect})$ 来进行校正。

在图8中，实际上该产品的整体违约率只有2%左右，而评分卡开发样本的违约率为10%。因此可以通过这种方式对每个分数区间的Odds予以校准。

图 8 - 基于Odds的评分卡校准

Part 4. 如何定量评估校准的好坏？

我们通常用对数损失函数(Logarithmic Loss，LL)和Brier分数（Brier score，BS）来衡量校准质量，分别定义如下：

$\left\{ \begin{aligned} Log\_Loss = -\sum_{i=1}^{N}(y_i * log(p_i) + (1-y_i)*log(1-p_i)) \\ Brier\_Score = \frac{1}{N}\sum_{i=1}^{N}(y_i - p_i)^2 \\ y_i \in \{0,1\} : actual \space\space class \space\space label\\ p_i \in [0,1] : \space\space estimated \space\space default \space\space probability \\ \end{aligned} \right. \tag{3}$

观察LL可知，当真实label=0，预测概率为1时，损失函数将达到+∞。LL惩罚明显错误的分类。当预测概率越接近于真实标签，LL越小，模型的校准效果就越好。
观察BS可知，当BS指标越小，代表模型预测结果越接近于真实标签。

因此，这两个指标都反映样本集上真实标签与预测概率之间的差异性（也就是一致性）。

这里，我们就有了答案：LR在参数估计时所用到的损失函数正是对数损失函数，故而才具有良好的校准度。

LogisticRegression returns well calibrated predictions as it directly optimizes log-loss.

Part 5. 概率分数尺度变换成整数分数

至此，我们已经掌握了如何对模型输出概率进行校准，但还不是文章开头所见的整数分。现在，介绍将概率分数尺度变换（scaling）成整数分数。在很多信用评分书籍中，有时也会并不加以区分地称为风险校准，但并不恰当。

这是非常有用的，因为从业务上很难理解一个概率分代表的含义，但人们对于整数分更容易接受。比如，温度计上的刻度 ️。单调性保证了映射过程不会改变分数的排序性。

图 9 - 评分卡赋分

为简化处理，我们只考虑一个自变量X，那么逻辑回归定义如下：

$ln(Odds) = ln(\frac{p(Y=Bad|X)}{p(Y=Good|X)}) = ln(\frac{p}{1-p}) = w * WOE(x) + b \tag{4}$

在《WOE与IV指标的深入理解应用》一文中，我们认识到WOE变换是一个分段函数，其把自变量x与y之间的非线性关系转换为线性关系。若把WOE定义如下，那么含义为：自变量x在经过WOE变换后，取值越大，预测为bad的概率越高。

$WOE(x) = \left\{ \begin{aligned} woe_1 = ln(\frac{Bad_1}{Good_1}) - ln(\frac{Bad_T}{Good_T}) , x \in bin_1\\ woe_2 = ln(\frac{Bad_2}{Good_2}) - ln(\frac{Bad_T}{Good_T}) , x \in bin_2\\ ... \\ woe_m = ln(\frac{Bad_m}{Good_m}) - ln(\frac{Bad_T}{Good_T}) , x \in bin_m \\ \end{aligned} \right. \tag{5}$

我们会发现在2个地方出现了Odds的身影——LR的左边和WOE变换。

此时，由于两者的Odds（几率）的定义是坏好比，也就是“坏人概率 / 好人概率”。因此，在参数估计时，自变量前的权重系数w的符号是正的。实践中发现不少人搞不清楚为什么有时候是正号，有时候是负号。问题主要在于WOE和LR中Odds定义是否一致。

当WOE中定义Odds是好坏比时，w系数为负；
当WOE中定义Odds是坏好比时，w系数为正；

将LR输出线性映射为信用分的公式如下，通常将常数A称为补偿，常数B称为刻度。

$define \left\{ \begin{aligned} A > 0, B > 0 \\ Odds = \frac{p(Y=Bad|X)}{p(Y=Good|X)} = \frac{p}{1 - p} \\ \end{aligned} \right. \\ \Rightarrow credit\_score = A - B * ln(Odds) \\ \Rightarrow credit\_score = A - B * [\beta_0 + \beta_1 * WOE(x)] \tag{6}$

在上式中，由于Odds是坏好比，Odds越大，代表bad的概率越高；而信用分越高，代表bad的概率越低。两者业务含义上相反，因此是减号。

我们需要定义三个必要的参数：

1. 基准Odds：与真实违约概率一一对应，可换算得到违约概率。
2. 基准分数：在基准Odds时对应的信用分数。
3. PDO:（Points to Double the Odds）：Odds（坏好比）变成2倍时，所减少的信用分。

接下来，我们就可以求解出A和B，过程如下：

$define \left\{ \begin{aligned} PDO > 0 \\ A > 0, B > 0 \\ Odds = \frac{p(Y=Bad|X)}{p(Y=Good|X)} = \frac{p}{1 - p} \\ \end{aligned} \right. \\ \Rightarrow \left\{ \begin{aligned} base\_score = A - B * ln(Odds_0) \\ base\_score - PDO = A - B * ln(2 * Odds_0) \\ \end{aligned} \right. \\ \Rightarrow \left\{ \begin{aligned} B = \frac{PDO}{ln(2)} \\ A = base\_score + \frac{PDO}{ln(2)} * ln(Odds_0) \\ \end{aligned} \right. \\ \tag{7}$

现以具体数字来说明。假设我们希望信用分base_score为600时，对应的Odds（坏好比）为1:50。而当Odds扩大2倍至2:50时，信用分降低20分至580分（PDO=20）。那么：

$\left\{ \begin{aligned} B = \frac{PDO}{ln(2)} = \frac{20}{ln(2)} = 28.8539 \\ A = base\_score + \frac{PDO}{ln(2)} * ln(Odds_0) = 600 + 28.8539 * ln(1/50) = 487.122\\ \end{aligned} \right. \\ \Rightarrow \Rightarrow credit\_score = 487.122 - 28.8539 * ln(Odds) \\ \Rightarrow credit\_score = 487.122 - 28.8539 * (w * WOE(x) + b) \tag{8}$