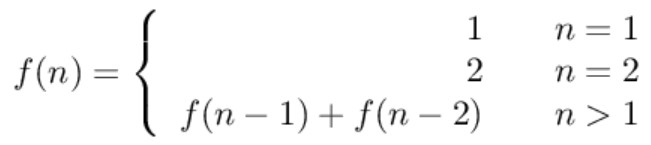描述
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,从同一个方向看总共有多少种不同的方法?
比如n=3时,2*3的矩形块有3种不同的覆盖方法(从同一个方向看):
输入描述:
2*1的小矩形的总个数n
返回值描述:
覆盖一个2*n的大矩形总共有多少种不同的方法(从同一个方向看)
示例1
输入:
0
返回值:
0
示例2
输入:
1
返回值:
1
示例3
输入:
4
返回值:
5
==================================================================================================================================
解题思路:
本题为动态规划问题,掌握规律
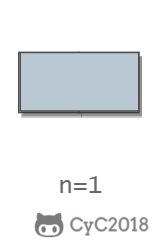
当 n 为 1 时,只有一种覆盖方法:
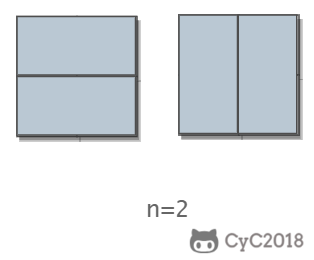
当 n 为 2 时,有两种覆盖方法:
要覆盖 2*n 的大矩形,可以先覆盖 2*1 的矩形,再覆盖 2*(n-1) 的矩形;或者先覆盖 2*2 的矩形,再覆盖 2*(n-2) 的矩形。而覆盖 2*(n-1) 和 2*(n-2) 的矩形可以看成子问题。该问题的递推公式如下: